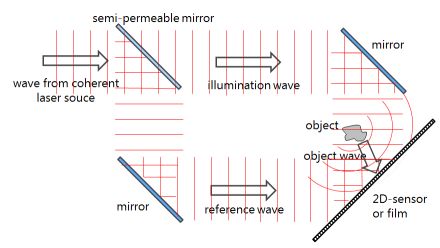
Terahertz radiation is electromagnetic radiation between the microwave and infrared band. It penetrates a wide variety of non-conducting materials. Here we describe holographic techniques to increase the resolution beyond the wavelength restrictions of classical imaging.
Holographic principle
Object can be reconstructed if intensity and phase of the diffracted object wave are known in the detector plane.
Phase determination
After subtraction of the thermal background the interferometric signal recorded by the camera is
where subscripts ref and obj refer to the THz reference beam and the object beam, respectively. φ is the respective phase of the waves, while δφ denotes a phase step controlled by mirror translation. In order to reconstruct the object, knowledge of the amplitude and the phase of the object wave is a prerequisite.
While its amplitude is readily available from the diffraction pattern (taking the square root of the intensity of the object wave measured without reference beam), the phase of the object wave is retrieved either using phase stepping algorithms (PSA) or applying the Fourier transform method (FTM) to the carrier frequency frames. PSA retrieve the phase in every image pixel individually by using a set of images each with a varied optical path difference between the object and reference wave. FTM uses a single interference image with a carrier fringe induced by an off-axis reference beam and retrieves the phase from its Fourier transform.
Image reconstruction
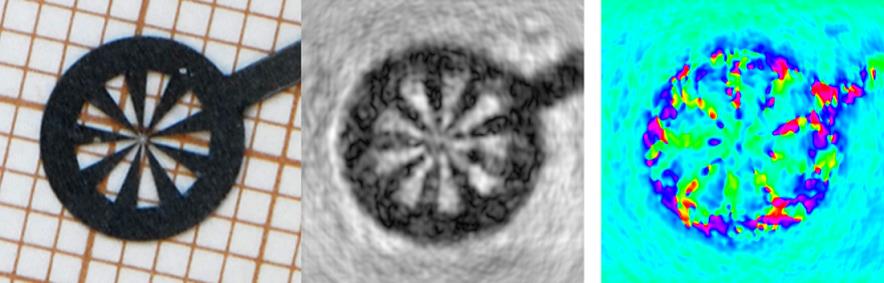
The reconstruction method is based on evaluating the Rayleigh-Sommerfeld diffraction integral by use of the fast Fourier transform. The reconstructed complex field at the object plane is obtained by backpropagated to a plane parallel or tilted plane at a given distance and tilt angle.
