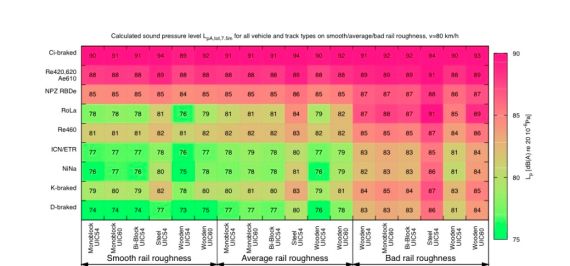
The emission model yields sound power levels for five predefined source heights along the vehicle surface for each vehicle in dependence of infrastructure and operation conditions. Track sections with constant properties, i.e. track superstructure, travelling speed, traffic volume and composition, are combined to line source segments that can be described by their total sound power.
The emission model describes rolling noise as the primary sound source based on roughness spectra of wheel and rail. First an effective roughness spectrum is derived using a contact patch filter that takes into account the contact area of wheel and rail. In combination with train speed and type-dependent transfer-functions for wheel and track, the total rolling noise can then be calculated. Special solutions are implemented for switches, several types of bridges and curved tracks.
Secondary sound sources such as traction noise, gear noise or aerodynamic noise are described by a speed dependent sound power spectrum. .
The following aspects are not taken into account in the emission model: noise at railway stations, accelerating and decelerating vehicles, braking noise and curve squeal. For further information it is referred to the publication of the sonRAIL emission model.

The propagation model is organized in four different modules that are operated independently from each other. The module ‘Basic’ is mandatory for each calculation as it determines direct sound propagation under the assumption of a homogenous atmosphere. Air absorption is taken into account according to the ISO Standard 9613-1. Ground reflections are calculated for spherical waves over flat and homogenous ground. The solution is extended to uneven terrain and varying ground properties using a Fresnel-zone-approach and accounts for the coherence loss between direct and reflected sound in dependence of frequency and propagation distance. Shielding effects can either be considered according to ISO 9613-2 or according to a method presented by A.D. Pierce., Foliage attenuation is determined according to ISO 9613-2.
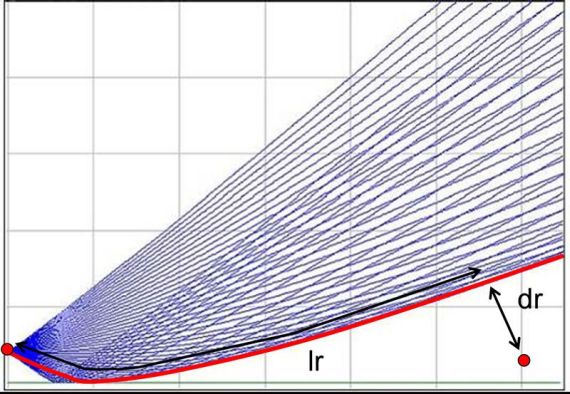
In the second module, meteorological effects on sound propagation are accounted for. As additional input data vertical profiles of wind speed, temperature and humidity are used. While temperature and humidity influence air absorption, vertical wind and temperature gradients in combination with wind direction are used to derive effective sound speed profiles. Based on these sound speed profiles a ray tracing algorithm is applied to estimate changes in shielding effect and the evolution of acoustical shadow zones as a consequence of sound propagation along curved rays.

The third and fourth module calculate additional sound energy contributions, one from reflections at buildings, walls and other rigid surfaces and one from diffuse reflections at forest edges and cliffs. The model for reflections at buildings, walls and other rigid surfaces is designed for sound propagation in urban environments. The calculation procedure is based on two analytical solutions of the reflection problem, one for coherent reflections (specular reflections) and one for scattering.
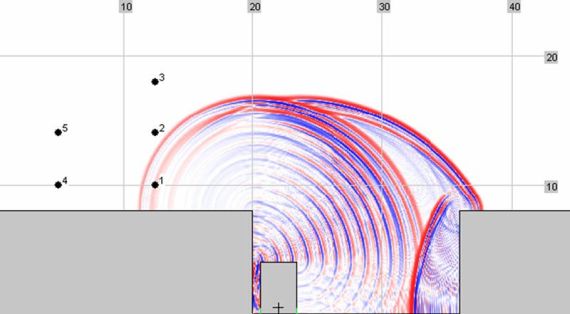
In principle sound propagation is independent of the type of sound source. Nevertheless there are phenomena that are specific for a certain source type. For railway noise this is for example the case for the ground effect close to the source that shows a distinct behavior as a consequence of the specific properties of the ballast bed. Therefore an extended ground effect model is implemented for this situation. Also typical for railway noise are situations with hard surfaces in close vicinity of the vehicles that lead to additional reflections. This is for example the case for tunnel openings or railway line cuttings, as shown below. In order to reduce the calculation effort, these multiple reflections are not dealt with within the reflection module but are treated based on empirical formulas.
For more detailed information about the model it is referred to the description of the sonRAIL propagation model.

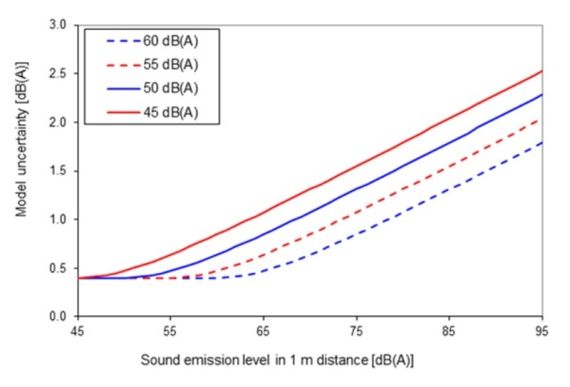
The accuracy of the sonRAIL model has been discussed in detail in the project documentation. The uncertainty is thereby assessed separately for the emission and the propagation model under the assumption, that the necessary input parameters are not available in any detail but with reasonable accuracy. On the other hand an averaging over several train pass-by’s is considered, as it is the case in the assessment of noise limits on the basis of long-term averages. The partial uncertainties of the two models can be assumed to be independent and are summed up according to the rules of error propagation. Based on comparisons of measurements in 7.5 m distance from the track center line according to ISO 3095 with calculations, an standard deviation of the emission model of 0.4 dB(A) was derived. The validation of the propagation model showed that the uncertainty of the propagation calculation exhibits proportionality to the overall sound attenuation. Comparing the sound exposure level with an emission level in a reference distance of 1 m, a standard deviation of the calculation model error of 5 % of the reference sound attenuation was derived. In the Figure below, the resulting prognosis uncertainty in dependence of the emission level is depicted for four different equivalent continuous sound pressure levels Leq. The higher the emission, the greater is the distance where a certain immission level is reached and consequently the greater is the uncertainty of the prognosis. For emission levels typical for busy lines, the model accuracy for the assessment of noise rating levels according to the Swiss noise limits amounts to less than 2 dB(A).