Contrast formation in the MFM ideally is the result from the interaction of an extended magnetic tip with the stray field gradients of the sample. For convenience the process is described in coordinates k = (k_x, k_y) of the 2D reciprocal-space for the scan plane, and direct space for the tip-sample distance z along the scan plane normal. It can be shown [6] that the MFM signal Δf(k,z) measured at tip-sample distance z for a stray field H_z(k,z)  depends on the instrument calibration function ICF(k,z)  as

The ICF(k,z) includes terms for the geometry and orientation of the cantilever, as well as its mechanical and magnetic properties. Importantly, it includes  information on the spatial distribution of the magnetic charges of the MFM tip.

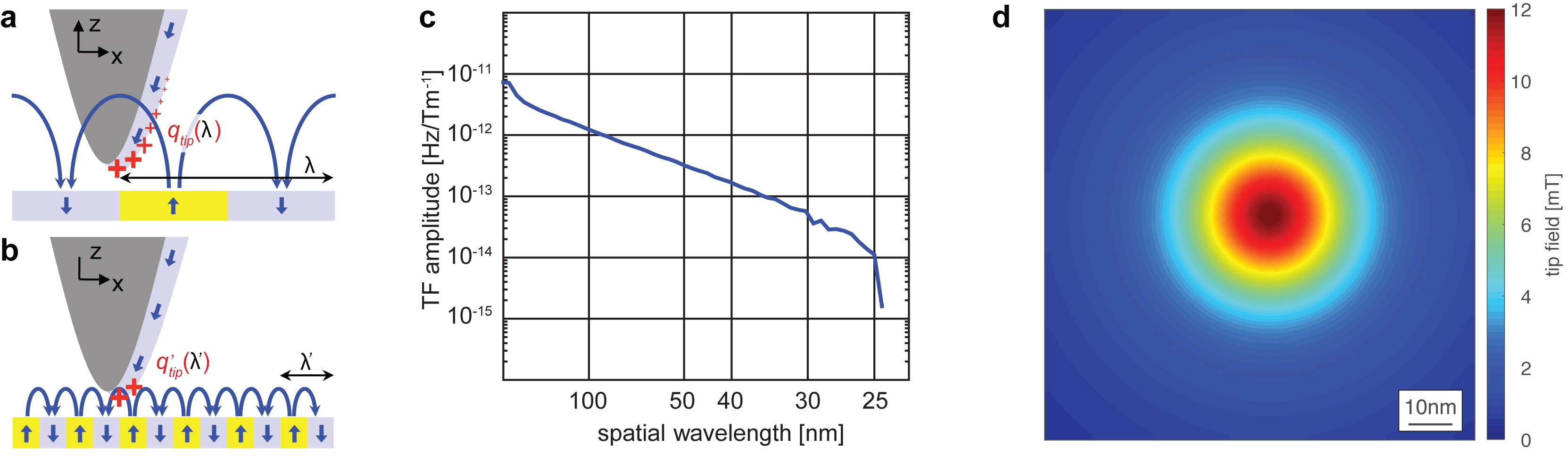
Calibrating the instrument or the tip is essentially an inversion of Equation (2). We determine the ICF(k,z) from a sufficiently large number of MFM scans of domains with narrow domain walls through thickness perpendicular domains from a suitable thin film calibration sample with perpendicular magnetic anisotropy [7]. All MFM Δf -images have been acquired at the same tip-sample distance. Recall that stray fields of a thin film sample are subject to so-called distance losses [8,9], which describe a rapid decrease with distance of the field amplitude for high spatial frequencies in the field (exponential factors of –k ∙ z). The ensuing unequal degradation of the SNR for high and low spatial frequencies is a practical restriction of the usefulness of Eq. (1) for high frequencies, i.e. small magnetic features. A further evident difficulty connected to distance losses is that the measured amplitudes vary strongly with distance, so that maintaining stability of the scan plane is essential. For tip-sample distance control we rely on capacitive excitation of the second flexural cantilever oscillation mode [5]. With this, the tip-sample distance can be kept constant within to ±0.5 nm over several hours, and even if the measurement temperature or the applied external field is changed.

Because the MFM scans a space devoid of sources of magnetic field, in practice we can write the latter as the gradient of a magnetic potential, , where  satisfies the Laplace equation. For definiteness we assume the sources of the stray field (provided by the sample) are described by a boundary condition on the xy-plane, parallel to the scan plane located at distance z from the top surface of the sample. In the 2D Fourier space utilized in the previous section, this leads to the convenient expression

and therefore also to